Experimenting with RNN!
This experiment has been run on an NVIDIA GeForce GTX 970 but shouldn’t have any problem using CPU only.
This experiment is written in Python with the help of the libraries Tensorflow and Keras; the model code exist on a different file to make this easier to run. See the (DeepLearningModels.py) file for complete code.
Feedforward and Recurrent neural networks
Feedforward neural networks can approximate any continuous function, but only in the interval with enough training data density (Universal approximation theorem). Unlike feedforward neural networks, RNNs can use their internal states (memory) to store information from the input and the histories.
Method: The dataset is two different sine waves multiplied together to create the wave we want to predict. We train two models, a Feedforward neural network and an RNN, on this dataset. We send the predicted values back to the model to follow if the model has learned the function.
Hypothesis: Feedforward neural networks accuracy is expected to go down for every period, while RNN would remember.
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.ticker import MaxNLocator
from DeepLearningModels import ModelFullyConnected, ModelRNN, sine_wave
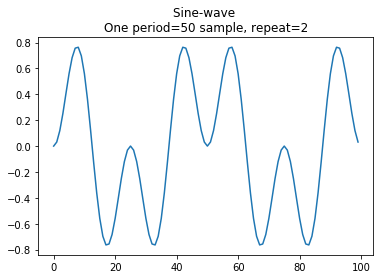
Sine wave
wave_1 = sine_wave(nsamples=50, periods=1, repeat=2)
wave_2 = sine_wave(nsamples=50, periods=2, repeat=2)
data = wave_1*wave_2
plt.title('Sine-wave \nOne period=50 sample, repeat=2')
plt.plot(data)
plt.show()
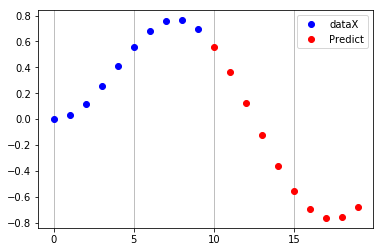
Create features and targets
time_back = 10
time_forward = time_back
batch_size = 1
dataX, dataY = [], []
for i in range(len(data)-time_back-time_forward):
dataX.append(data[i:i+time_back])
dataY.append(data[i+time_back:i+time_back+time_forward])
dataX = np.array(dataX)
dataY = np.array(dataY)
ax = plt.figure().gca()
ax.plot(range(time_forward), dataX[0], 'bo', label='dataX')
ax.plot(range(time_forward, 2*time_forward), dataY[0], 'ro', label='Predict')
ax.xaxis.set_major_locator(MaxNLocator(5, integer=True))
plt.legend()
plt.grid(axis='x')
dataX = dataX.reshape(len(dataX), batch_size, time_back)
print('dataX:', dataX.shape,'\ndataY:', dataY.shape, sep='')
dataX:(80, 1, 10)
dataY:(80, 10)
Create the models
fc_model = ModelFullyConnected(batch_size, dataX.shape, dataY.shape)
rnn_model = ModelRNN(batch_size, dataX.shape, dataY.shape)
Fully connected neural network
fc_model.create_model(nr_layers=3, units=30)
fc_model.fit(dataX, dataY)
fc_model.plot_training()
SimpleRNN
rnn_model.create_model(nr_layers=3, units=20)
rnn_model.fit(dataX, dataY)
rnn_model.plot_training()
Plot
plot_fc = fc_model.plot_predict(dataX[0:1], time_forward, len_range=100)
plot_rnn = rnn_model.plot_predict(dataX[0:1], time_forward, len_range=100)
plot_full = []
while len(plot_fc) > len(plot_full):
plot_full.extend(data)
plt.figure(figsize=(10, 7))
plt.subplot(211)
plt.title(fc_model.model_information())
plt.plot(plot_full[time_forward:len(plot_fc)], 'r--')
plt.plot(plot_fc[:-time_forward], 'b')
plt.subplot(212)
plt.title(rnn_model.model_information())
plt.plot(plot_full[time_forward:len(plot_fc)], 'r--')
plt.plot(plot_rnn[:-time_forward], 'b')
plt.tight_layout()
plt.show()
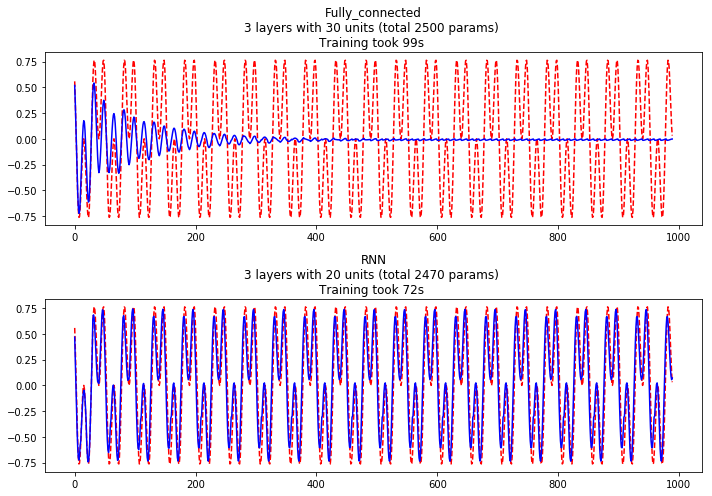
Conclusion: Feedforward neural networks are not great on data that have has a periodic quality. However, RNN can remember and have a “memory” about what they have “seen” before.
Discussion: When the Feedforward neural network model tries to predict the next value at zero, it has learned that the possibility is fifty-fifty. But the RNN model remembers the amplitude and frequency.
ToDo:
- Here are some ideas that I think are worth exploring:
- Change the value “time_back”, what is the lowest value?
- Try different activations.
- If the model is stateful, will it “remember” some aspects of the previous steps in the sequence.
- LSTM Vanishing gradient problem
- CNN